Seata 改良的雪花算法
前言
在 分布式 ID 生成方案 中,我们说了标准版的雪花算法,也提到了雪花算法严格依赖时钟的缺陷,并且给出了一个解决方案,最近看 Seata 相关内容的时候,发现 Seata 针对这个问题改进了雪花算法,所以这篇文章就来详细说一说。
标准雪花算法的问题
在这篇文章中,提到了标准雪花算法的两个问题:
- 时钟敏感
- 突发性能有上限
所谓时钟敏感,我们知道雪花算法的单调生成与系统时间戳的单调递增特性密切相关,所以如果出现时钟回拨(时钟漂移),那么就可能导致发号重复。
其次是雪花算法的突发性能有上限,标准的雪花算法中,序列号的长度是 12 位,所以毫秒内可以提供 4096 个序列号,而标准雪花算法宣称生成 QPS 可以达到 400w/s,这实际上这两者是不同的,前者要求每一毫秒的并发不得高于 4096,如果毫秒内的序列空间耗尽,只能自旋等待下一个时间戳。
Seata 如何改进
Seata 改进的雪花算法将 41bit 的时间戳和 10bit 的标识位交换了位置,并且只在初始化时获取当前系统的时间戳,之后无需与系统时间保持同步,只由序列号递增作为发号驱动。
当序列号溢出 12 位空间,则加到时间戳上,序列号归零,这样就突破了 4096/ms 的性能瓶颈。
就像下面这样:
- 1 bit(保留)+ 10 bit(标识位)+ 41 bit(时间戳)+ 12 bit(序列号)
所以这样改进有三点好处:
- 算法不再强依赖系统时钟,允许出现时钟漂移,仅在重启时的大幅度时钟回拨(人为或者修改系统时区)在可能出现发号重复,一般而言时钟漂移都是毫秒级别。
- 算法不存在 4096/ms 的突发性能限制。
- 时间戳和序列号相邻,可以使用 AtomicLong 进行递增,编码简单。
改进之后出现的问题
我们稍微思考一下,其实可以提出至少两个问题:
- 改进的算法虽然不存在 4096/ms 的限制,但是否会因为过于“超前消费”使生成器内时间戳远超于系统时间,导致机器在重启后出现发号重复。
- 由于算法仅仅依赖初始化时的时间戳,所以当部署多个 TC 节点,无法保证全局递增,只能保证节点内递增。
针对第一点,官方的解释是:
理论上如此,但实际几乎不可能。要达到这种效果,意味该生成器接收的 QPS 得持续稳定在 400w/s 之上,说实话,TC 也扛不住这么高的流量,所以说呢,天塌下来有个子高的先扛着,瓶颈一定不在生成器这里。
针对第二点,由于标识位在高位,所以从全局视角来看,标识位大的节点生成的 id 一定大,和时间戳无关。
考虑下面的代码:
public static void main(String[] args) throws InterruptedException {
CountDownLatch latch = new CountDownLatch(3);
List<String> list = new CopyOnWriteArrayList<>();
for (long i = 0; i < 3; i++) {
long finalI = i;
new Thread(() -> {
IdWorker idWorker = new IdWorker(finalI);
for (int j = 0; j < 5; j++) {
list.add("[node" + finalI + "]" + " is : " + idWorker.nextId());
}
latch.countDown();
}).start();
}
latch.await();
for (String str : list) {
System.out.println(str);
}
}输出:
[node1] is : 9602431209541633
[node1] is : 9602431209541634
[node2] is : 18609630464282625
[node0] is : 595231954800641
[node2] is : 18609630464282626
[node0] is : 595231954800642
[node2] is : 18609630464282627
[node1] is : 9602431209541635
[node0] is : 595231954800643
[node1] is : 9602431209541636
[node2] is : 18609630464282628
[node1] is : 9602431209541637
[node0] is : 595231954800644
[node2] is : 18609630464282629
[node0] is : 595231954800645在全局视角来看,并不是单调递增的,当然如果只看单个节点,那么就是单调递增的。
改进的算法不影响初衷
针对改进的雪花算法不具备全局单调递增特性的问题,官方的解释如下:
改进后的算法的确不具备全局的单调递增特性,但这不影响我们的初衷(减少数据库的页分裂)。这个结论看起来有点违反直觉,但可以被证明。
新版的雪花算法虽然不具备全局的单调递增特性,但是在节点内是单调递增的,而我们知道标识位只占 10 位,所以,最多支持 1024 个节点,也就意味着最多划分出 1024 个子序列,每个子序列都是单调递增的。
对于数据库而言,也许它最初接受的 id 是无序的,来个各个节点的 id 都混杂在一起,就像下面这样:
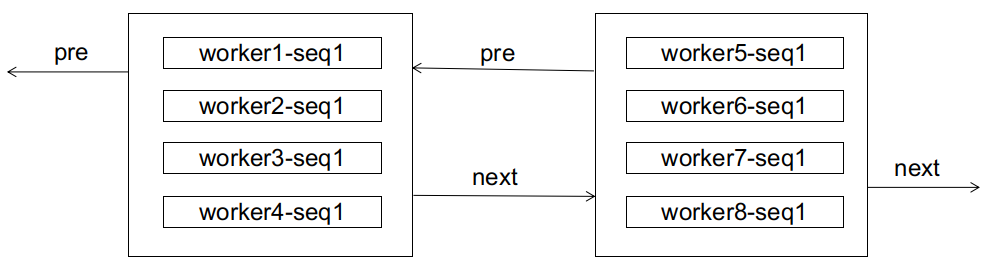
如果此时来了一个 worker1-seq2,显然会造成页分裂:
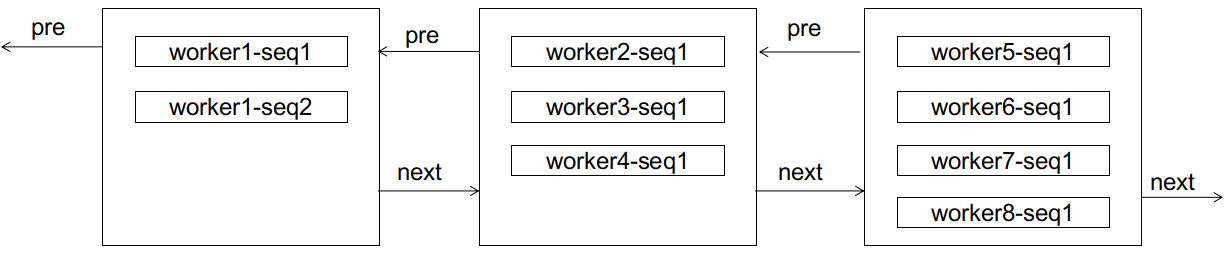
但分裂之后,有趣的事情发生了。
对于 worker1 而言,后续的 seq3,seq4 不会再造成页分裂(因为还装得下),seq5 也只需要像顺序增长那样新建页进行链接(区别是这个新页不是在双向链表的尾部)。
注意,worker1 的后续 id,不会排到 worker2 及之后的任意节点(因而不会造成后边节点的页分裂),因为它们总比 worker2 的 id 小;也不会排到 worker1 当前节点的前边(因而不会造成前边节点的页分裂),因为 worker1 的子序列总是单调递增的。
在这里,我们称 worker1 这样的子序列达到了稳态,意为这条子序列已经“稳定”了,它的后续增长只会出现在子序列的尾部,而不会造成其它节点的页分裂。
同样的事情,可以推广到各个子序列上。无论前期数据库接收到的 id 有多乱,经过有限次的页分裂后,双向链表总能达到这样一个稳定的终态:
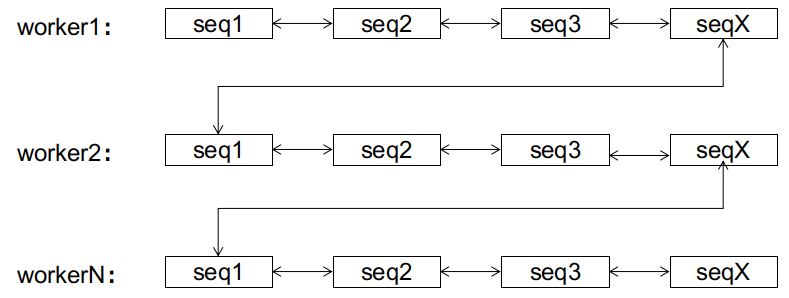
到达终态后,后续的 id 只会在该 id 所属的子序列上进行顺序增长,而不会造成页分裂。该状态下的顺序增长与 auto_increment 的顺序增长的区别是,前者有 1024 个增长位点(各个子序列的尾部),后者只有尾部一个。
所以,改进的算法从全局来看的确不是全局递增的,但该算法是收敛的,达到稳态后,新算法同样能达成像全局顺序递增一样的效果。
继续考虑数据的删除情况,数据的删除可能会导致页合并(Innodb 如果发现相邻 2 个数据页的空间利用率都不到50%,就会把它俩合并)
这对新算法的影响如何呢?
经过上面的流程,我们可以发现,新算法的本质是利用前期的页分裂,把不同的子序列逐渐分离开来,让算法不断收敛到稳态。而页合并则恰好相反,它有可能会把不同的子序列又合并回同一个数据页里,妨碍算法的收敛。
尤其是在收敛的前期,频繁的页合并甚至可以让算法永远无法收敛!但如果算法已经完成收敛,则只有在各个子序列的尾节点进行的页合并,才有可能破坏稳态(一个子序列的尾节点和下一个子序列的头节点进行合并)。而在子序列其余节点上的页合并,不影响稳态,因为子序列仍然是有序的,只不过长度变短了而已。
所以,如果在业务系统中使用新算法,需要确保算法有时间进行收敛。比如用户表之类的,数据本就打算长期保存的,算法可以自然收敛。或者也做了延迟删除的机制,给算法足够的时间进行收敛。
