二分搜索
7455字约25分钟
2024-10-20
前言
二分搜索类题目:
- 二分答案法应用
- LeetCode 轮转数组类题目
二分答案法
所谓二分答案法,就是估计最终答案可能的范围,这个范围初步可以定的粗略一些,反正后续求解会使用二分搜索,其实也二分不了几次。
其次是分析问题的答案和给定条件之间的单调性,大部分时候只需要用到自然智慧。
建立一个 f 函数,当有一个备选答案的情况下,判断给定的条件是否达标。
在最终答案可能的范围上不断二分搜索,每次二分的中点都用 f 函数判断,直到二分结束,找到最合适的答案。
核心点:分析单调性、建立 f 函数
爱吃香蕉的珂珂
首先,题目求解的最小速度 k 的取值是存在一个范围的,由于 piles[i] ≥ 1,所以 k 至少为 1,而 k 的最大值其实就是整个 piles 数组的最大值 max,因为如果 k > max,是不能吃下一堆香蕉的,必须要等待,所以 k 没有必要更大。
所以 k 的范围可以确定为:1 ~ max。
同时,随着 k 的增大,吃完全部香蕉的时间要么不变,要么减少,这是显而易见的,所以 k 和吃完香蕉的时间是存在单调性的,这是可以进行二分的基础。
到这里,还有一个关键点在于,如何判断 k 为具体某个值时是否满足题意。
对于本题目来说,如何判断 k 为某个值是是否满足题意,其实就是每一个位置的香蕉数除以 k 向上取整的商进行累加看是否 < h。
这里向上取整的写法:
- num1 和 num2 是非负整数
- 如果是 num1 / num2,这在计算机里面是向下取整
- 如果要向上取整,请写为 (num1 + num2 - 1) / num2
class Solution {
public int minEatingSpeed(int[] piles, int h) {
int max = 0;
for (int pile : piles) {
max = Math.max(max, pile);
}
int res = -1;
int l = 1, r = max, m;
while (l <= r) {
m = l + r >> 1;
if (f(piles, h, m)) {
r = m - 1;
res = m;
} else {
l = m + 1;
}
}
return res;
}
// 判断在 k = speed 的情况下,是否可以在 h 小时内吃完
public boolean f(int[] piles, int h, int speed) {
int need = 0;
for (int pile : piles) {
// pile / speed 的向上取整写法
// 务必记住
need += (pile + speed - 1) / speed;
if (need > h) {
return false;
}
}
return need <= h;
}
}分割数组的最大值
这道题目本质就是在求划分出来的这 k 个非空连续子数组中,最大的累加和的最小值,我们记为 ans。
那么 ans 最大值为整个数组的累加和,这是毋庸置疑的,因为需要将原数组划分为非空的子数组,所以 ans 的最小值是原数组的最小值。
那么 ans 的范围就是:min ~ sum,sum 表示整个数组的累加和,min 表示原数组的最小值。
我们给定一个函数 f,可以求出在数组 nums 上进行划分,需要满足划分后的各个子数组各自累加和的最大值为 limit 的情况下,至少需要划分为多少个子数组。
再次描述 limiit:对 nums 数组进行划分,得到 n 个子数组,这 n 个子数组各自的累加和的最大值为 limit。
随着 limit 的增大,子数组的长度一定要增大,划分的子数组数量要么不变,要么减少,这就是一个单调性。
所以,我们在 min ~ sum 上进行二分,根据 f 函数求出至少需要划分为 n 个子数组才能满足这 n 个子数组的累加和的最大值为 limit,若 n ≤ k,说明还需要继续划分,limit 要减小,继续向左二分,否则向右二分。
class Solution {
public int splitArray(int[] nums, int k) {
int sum = 0, min = Integer.MAX_VALUE;
for (int num : nums) {
sum += num;
min = Math.min(min, num);
}
int ans = -1;
int l = min, r = sum, m;
while (l <= r) {
m = l + r >> 1;
if (f(nums, m, k)) {
r = m - 1;
ans = m;
} else {
l = m + 1;
}
}
return ans;
}
// 在 nums 上进行划分,每个子数组的累加和 <= limit 时可以划分出的子数组的个数 n 是否 <= k
public boolean f(int[] nums, int limit, int k) {
int n = 1, tmp = 0;
for (int num : nums) {
if (num > limit) {
// 不能划分出子数组
return false;
}
if (tmp + num > limit) {
n++;
tmp = num;
} else {
tmp += num;
}
}
return n <= k;
}
}机器人跳跃问题
首先这道题求最少单位的初始能量,我们不妨想一下初始能量的范围。
毋庸置疑的是初始能量最少可以是 1(H 数组全为 1 的情况),至于初始能量的最大值为 H 数组的最大值,这样的话,每遇到 H 数组中的一个元素,能量值都会增加,最后肯定可以保证完成游戏。
所以,初始能量的范围为 1 ~ max。
所以我们在 1 ~ max 上进行二分,对二分的每一个值,都判断是否可以完成游戏,这实际上也是存在单调性的,如果值 k 可以完成游戏,那么对于 k + 1、k + 2 等一定也是可以完成游戏的。
最后就是定义一个 f 函数,表示当初始能量为 Init 时,是否可以保证完成游戏。
import java.io.*;
public class Main {
public static int MAXN = 100001;
public static int[] H = new int[MAXN];
public static int n = 0;
public static void main(String[] args) throws IOException {
StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
while (in.nextToken() != StreamTokenizer.TT_EOF) {
n = (int) in.nval;
int l = 1;
// r 也是最大值
int r = 0;
for (int i = 0; i < n; i++) {
in.nextToken();
H[i] = (int) in.nval;
r = Math.max(r, H[i]);
}
out.println(binary(l, r, r));
}
out.flush();
out.close();
}
private static int binary(int l, int r, int max) {
int mid;
int ans = -1;
while (l <= r) {
mid = l + r >> 1;
if (check(mid, max)) {
ans = mid;
r = mid - 1;
} else {
l = mid + 1;
}
}
return ans;
}
// 初始能量为 init 是否可以完成游戏,这里 max 主要是为了防止溢出
public static boolean check(int init, int max) {
for (int i = 0; i < n; i++) {
if (init > H[i]) {
init += (init - H[i]);
// 如果 init 很大,那么后续能量的增长可能是指数级别的
// 所以,一旦 init > max 则直接返回
if (init > max) return true;
} else {
init -= (H[i] - init);
if (init < 0) return false;
}
}
return true;
}
}找出第 K 小的数对距离
题目是求数对距离,我们不妨看看一个普遍数组中所有的数对距离可能的范围。
首先最小肯定是 0,那么最大的数对距离就是数组中的最大值 - 最小值。
所以数对距离的范围是:0 ~ max - min
定义一个 f 函数,可以求出数对距离为 dis 的情况下,数组中有多少组数对,其数对距离 ≤ dis。
显然,当 dis 增大,那么数组中符合条件的数对数量要么不变,要么增大。
所以不妨对数对距离 dis 在 0 ~ max - min 进行二分,根据 f 函数求出数对距离为 dis 的情况下,数组中有 n 组数对,其数对距离 ≤ dis,若 n ≥ k 则记录 ans 并向左二分,反之,向右二分。
最后,f 函数可以使用滑动窗口,但先决条件是数组有序,所以我们先对数组排序。
题解代码:
import java.util.Arrays;
class Solution {
public int smallestDistancePair(int[] nums, int k) {
Arrays.sort(nums);
int n = nums.length;
int l = 0, r = nums[n - 1] - nums[0], mid;
int ans = -1;
while (l <= r) {
mid = l + r >> 1;
if (count(nums, mid) > k) {
ans = mid;
r = mid - 1;
} else {
l = mid + 1;
}
}
return ans;
}
private int count(int[] nums, int dis) {
int ans = 0;
for (int winl = 0, winr = 0; winl < nums.length; winl++) {
while (winr + 1 < nums.length && nums[winr + 1] - nums[winl] <= dis) {
winr++;
}
ans += winr - winl;
}
return ans;
}
}同时运行 N 台电脑的最长时间
假设需要让这 n 台电脑运行 m 分钟,两个结论:
- 电池数组 batteries 中,元素值大于 m 的电池在整个供电的过程中为一台电脑供电就可以了。
- 对于全是碎片电池的电池数组(所谓碎片电池就是电量 batteries[i] < m),如果碎片电池的累加和 ≥ m * n,那么这些碎片电池一定可以使得这 n 台电脑运行 m 分钟。(通过辗转腾挪一定可以做到)。
结合第 1、2 点,对于一个普遍的电池数组,首先非碎片电池可以在 m 时间内各自运行一台电脑,剩余的非碎片电池再进行辗转腾挪看是否可以运行剩下的电脑。
举个例子:
电池数组为 [3, 4, 10, 12, 7, 8, 10, 9],问需要使用这些电池在 6 台电脑上运行 10 分钟,是否可行?
- 首先 2、3、6 号电池可以各自运行一台电脑,也就是 3 台电脑。
- 剩余的碎片电池的累加和为 31,是大于
10 * 3的,所以一定可以满足要求,是可行的。
接下来就是二分答案法的使用。
题目求这 n 台电脑运行的分钟数,那么它的最小值是 0,最大值是 batteries 数组的累加和(比如只有 1 台电脑)。
对于函数 f,其实就是我们上面的所说的,是否可以让这 n 台电脑运行 m 分钟。
显然,单调性是运行的分钟数越多,就更难达成目标。
所以,在 0 ~ sum 上进行二分,根据 f 判断是否可以让 n 台电脑运行 mid 分钟,如果可以,那么记录答案,继续向右二分,否则向左二分。
题解代码:
class Solution {
public long maxRunTime(int n, int[] batteries) {
long sum = 0;
for (int battery : batteries) {
sum += battery;
}
long l = 0, r = sum, mid;
long ans = -1;
while (l <= r) {
mid = l + r >> 1;
if (canRun(batteries, n, mid)) {
ans = mid;
l = mid + 1;
} else {
r = mid - 1;
}
}
return ans;
}
// 给定电池数组,是否可以让 n 台电脑运行 time 分钟
private boolean canRun(int[] batteries, int n, long time) {
// 碎片电池的累加和
long sum = 0;
for (int battery : batteries) {
if (battery > time) {
n--;
} else {
sum += battery;
}
}
return sum >= (long) n * time;
}
}一个小的贪心如下:
class Solution {
public long maxRunTime(int n, int[] batteries) {
long sum = 0;
int max = 0;
for (int battery : batteries) {
sum += battery;
max = Math.max(max, battery);
}
if (sum > (long) max * n) {
// 所有电池的最大电量是 max,若此时 sum > (long) max * n
// 表示最终的供电时间一定 >= max,而如果最终的供电时间 >= max,那么所有的电池都是碎片电池
// 那么尽可能大的供电时间就是 sum / n
return sum / n;
}
// 到这里,最终的供电时间一定是 < max,那么范围右边界得到优化
int l = 0, r = max, mid;
int ans = 0;
while (l <= r) {
mid = l + r >> 1;
if (canRun(batteries, n, mid)) {
ans = mid;
l = mid + 1;
} else {
r = mid - 1;
}
}
return ans;
}
// 给定电池数组,是否可以让 n 台电脑运行 time 分钟
private boolean canRun(int[] batteries, int n, int time) {
// 碎片电池的累加和
long sum = 0;
for (int battery : batteries) {
if (battery > time) {
n--;
} else {
sum += battery;
}
}
return sum >= (long) n * time;
}
}在 D 天内送达包裹的能力
我们考虑在 days 天内将传送带上的所有包裹送达的船的最低运载能力,其最小值是 weight 数组的最大值,最大值是 weight 数组的累加和。
所以最低运载能力的范围:max ~ sum
考虑函数 f 为在运载能力为 pow 的情况下,将包裹运完至少需要多少天。
显然,pow 越大,包裹运完需要的天数要么不变,要么减少,这就是单调性。
所以,我们考虑在 max ~ sum 进行二分,每一次的 mid 值通过 f 函数求出至少需要 n 天,若 n ≤ days,则记录 ans 并继续向左二分,否则向右二分。
题解代码:
class Solution {
public int shipWithinDays(int[] weights, int days) {
int sum = 0, max = 0;
for (int weight : weights) {
sum += weight;
max = Math.max(max, weight);
}
int l = max, r = sum, mid;
int ans = -1;
while (l <= r) {
mid = l + r >> 1;
if (leastDays(weights, mid) <= days) {
ans = mid;
r = mid - 1;
} else {
l = mid + 1;
}
}
return ans;
}
private int leastDays(int[] weights, int pow) {
int ans = 0;
int i = 0;
while (i < weights.length) {
if (pow < weights[i]) {
return Integer.MAX_VALUE;
}
int sum = 0;
while (i < weights.length && sum + weights[i] <= pow) {
sum += weights[i++];
}
ans++;
}
return ans;
}
}制作 m 束花所需的最少天数
根据题意,要求摘 m 束花等待的最少时间,我们不妨看看摘 m 束花等待的时间的范围。
首先最小值,由于 m 最小为 1,所以摘 m 束花等待的时间最小为 1,对于最大值,存在结果的情况下,最大值为 bloomDay 数组的最大值,到这个时候,所有的花都可以使用了,必然满足。
接下来考虑函数 f,f 表示在等待时间为 waitTime,可以摘的花的数量。
对于单调性来说,一旦等待时间 waitTime 增大,那么必然摘的花的数量要么不变,要么增大,这就是单调关系。
所以,我们可以在 1 ~ max 的范围内进行二分,根据 f 求出在等待时间为 mid 时可以摘的花的数量 n,若 n ≥ m,那么记录 ans,并继续向左进行二分,反之,继续向右进行二分。
题解代码:
class Solution {
public int minDays(int[] bloomDay, int m, int k) {
if (m * k > bloomDay.length) return -1;
int max = 0;
for (int num : bloomDay) {
max = Math.max(max, num);
}
int l = 1, r = max, mid;
int ans = -1;
while (l <= r) {
mid = l + r >> 1;
if (getFlowers(bloomDay, mid, k) >= m) {
ans = mid;
r = mid - 1;
} else {
l = mid + 1;
}
}
return ans;
}
// 在 waitTime 时间内可以采摘的花束的数量,滑动窗口
private int getFlowers(int[] bloomDay, int waitTime, int k) {
int ans = 0;
for (int winl = 0, winr = 0; winr < bloomDay.length; winr++) {
while (winr < bloomDay.length && bloomDay[winr] <= waitTime) {
winr++;
}
ans += (winr - winl) / k;
winl = winr + 1;
}
return ans;
}
}H 指数 II
对于 h 指数来说,其最小值是 0,比如研究者的所有论文都被引用了 0 次,最大值是 citations 数组的长度,毕竟该研究者只有 citations.length 篇论文。
所以,h 指数的范围是:0 ~ citations.length
对于 f 函数来说,f 表示 h 指数为 p 的情况下,判断是否有 p 篇文献被引用的次数为 p,由于数组已经是升序,那么 f 函数可以通过$ O(1) $的时间复杂度得到。
显然,h 指数越小,f 函数越容易得到满足,这也就是一种单调性。
所以,我们在 0 ~ citations.length 范围内进行二分,如果 h 指数为 mid 的情况下,已经满足条件(f 函数返回 true),那么记录 ans,继续向右二分,反之,向左二分。
class Solution {
public int hIndex(int[] citations) {
int l = 0, r = citations.length, mid;
int ans = -1;
while (l <= r) {
mid = l + r >> 1;
if (check(citations, mid)) {
ans = mid;
l = mid + 1;
} else {
r = mid - 1;
}
}
return ans;
}
// 判断是否有 p 篇文献被引用的次数为 p
private boolean check(int[] citations, int p) {
if (p == 0) return citations.length > 0;
return citations[citations.length - p] >= p;
}
}乘法表中第 k 小的数
题目求乘法表中的数字,显然数字的范围是在 1 ~ m * n。
所以我们定义函数 f,表示为给定一个值 num,求 num 是第几小的数字,或者说,num 前面有几个数比它小(这里是相对于乘法表中的元素来说)。
显然,值越大,那么前面比它小的数就越多,这就是单调性。
所以,在 1 ~ m * n 范围上进行二分,根据函数 f 求出二分中点是第 m 小的数字,若 m ≥ k 则记录 ans,继续向左二分,否则向右二分。
那么本题的关键其实在于函数 f 如何编写?
我们可以遍历乘法表的每一行,对于乘法表的第 i 行,其数字均为 i 的倍数,因此不超过 num 的数字有 min(num / i, n) 个,所以整个乘法表中不超过 num 的数字个数为 ∑i=1mmin(x/i,n)。
题解代码:
class Solution {
public int findKthNumber(int m, int n, int k) {
int l = 1, r = m * n, mid;
int ans = 0;
while (l <= r) {
mid = l + r >> 1;
if (getRank(mid, m, n) >= k) {
ans = mid;
r = mid - 1;
} else {
l = mid + 1;
}
}
return ans;
}
private int getRank(int num, int m, int n) {
int ans = 0;
for (int i = 1; i <= m; i++) {
ans += Math.min(num / i, n);
}
return ans;
}
}有序矩阵中第 K 小的元素
题目要求第 k 小的元素,显然结果的范围在 matrix[0][0] ~ matrix[n - 1][n - 1] 中。
所以我们定义函数 f,表示给定一个数 num,求出 num 在矩阵中的排名 rank(num 位于第 rank 个元素)
显而易见的是,数 num 越大,那么 rank 就越大,这就是单调性。
所以,我们考虑在 matrix[0][0] ~ matrix[n - 1][n - 1] 范围上进行二分,根据函数 f 求出二分中点的排名为 rank,若 rank ≥ k,则记录 ans 并继续向左二分,否则继续向右二分。
接下来,主要考虑 f 函数如何实现?
假设一个矩阵如下:
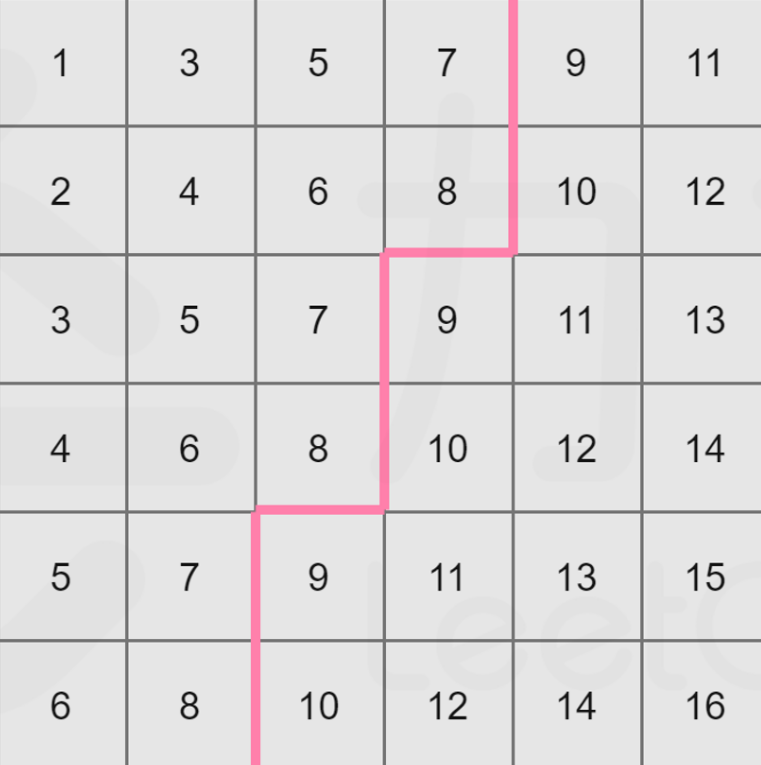
对于 8 来说,矩阵中 > 8 和 ≤ 8 的数分成了两个区域,那么左上区域的数量就是数值 8 的排名 rank。
所以
- 初始位置在
matrix[n - 1][0]处(左下角) - 来到每一个位置
matrix[i][j],若matrix[i][j] ≤ m则将当前列 ≤ m 的数的数量(即 i + 1) 累加到答案中,并向右移动,否则向上。 - 不断移动直到走出格子。
题解代码:
class Solution {
public int kthSmallest(int[][] matrix, int k) {
int n = matrix.length;
int l = matrix[0][0], r = matrix[n - 1][n - 1], mid;
int ans = 0;
while (l <= r) {
mid = l + ((r - l) >> 1);
if (getRank(matrix, mid) >= k) {
ans = mid;
r = mid - 1;
} else {
l = mid + 1;
}
}
return ans;
}
public int getRank(int[][] matrix, int num) {
int ans = 0;
int n = matrix.length;
int i = n - 1, j = 0;
while (i >= 0 && j < n) {
if (matrix[i][j] <= num) {
ans += i + 1;
j++;
} else {
i--;
}
}
return ans;
}
}修车的最少时间
题目要求修理所有汽车的时间 time,不妨考虑 time 可能的的范围。
首先 time 的最小值为 1(汽车数量为 1,且 ranks[i] = 1),time 的最大值为 rinks[0] * cars * cars(假设将所有的汽车都交给 0 号工人修理,那么耗费的时间就是 rinks[0] * cars * cars,更不用说还会有其他工人分担修汽车的任务)。
对于函数 f,表示给定时间 time 内,求最多可以修理车辆的数量。
显然,如果给定的时间越多,那么可以修理的汽车数量就越多,这就是单调性。
所以,考虑在 1 ~ rinks[0] * cars * cars 范围进行二分,根据 f 函数求出给定时间为 mid 时可以修理的汽车数量 n,若 n ≥ cars,则记录答案,继续向左二分,否则向右二分。
题解示例
class Solution {
public long repairCars(int[] ranks, int cars) {
long l = 1, r = (long) ranks[0] * cars * cars, mid;
long ans = -1;
while (l <= r) {
mid = l + ((r - l) >> 1);
if (getRepairByTime(ranks, mid) >= cars) {
ans = mid;
r = mid - 1;
} else {
l = mid + 1;
}
}
return ans;
}
public long getRepairByTime(int[] ranks, long time) {
long ans = 0;
for (int rank : ranks) {
ans += (long) Math.sqrt((double) time / rank);
}
return ans;
}
}打家劫舍 IV
要求窃取能力 cap 的最小值,不访考虑一个范围,cap 最大不过是 nums 的最大值 max,最小不过是 nums 的最小值 min。
存在的一个单调性是当 cap 变大,那么窃取的房屋数量一定会增加的,当然可能不是严格递增。
所以我们在 [min, max] 范围内进行二分,定义 f 函数表示在 nums 中偷窃,当窃取能力是 x 时,所能偷窃的最多的房屋数量 cnt,如果 cnt ≥ k,则记录答案,继续向左二分,找出更小的窃取能力,否则向右二分。
下面给出 f 函数,如何快速求出能窃取的最多的房屋数量 cnt
// 在 nums 数组上进行偷窃,偷窃的最大能力是 cap,返回最多可以偷窃多少家房屋
public int rob(int[] nums, int cap) {
int res = 0;
for (int i = 0; i < nums.length; i++) {
// 可以窃取则直接窃取
if (nums[i] <= cap) {
// 结果 +1
res++;
// 下一间房屋就不能窃取了
i++;
}
}
return res;
}这样的贪心策略(能早窃取就早窃取)为什么是正确的?
比如 [3, 4, 5] 的最大窃取能力是 10,那么是偷窃 3 还是偷窃 4 呢?如果偷窃 3 就放弃了 4,但是仔细一想,偷窃 3 或者偷窃 4 对结果(能够窃取的最多的房屋数量)的贡献都是 1,但是偷窃 3 的优势在于,如果 4 后面还有房屋,那么就可以继续偷窃。
所以遇到能偷就偷,不管下一个是否能偷窃,都将下一个房屋跳过。
class Solution {
public int minCapability(int[] nums, int k) {
int max = Integer.MIN_VALUE, min = Integer.MAX_VALUE;
for (int num : nums) {
max = Math.max(max, num);
min = Math.min(min, num);
}
// 在 [min...max] 范围内做二分搜素
int l = min, r = max, m;
int cap = -1;
while (l <= r) {
m = l + r >> 1;
if (rob(nums, m) >= k) {
cap = m;
r = m - 1;
} else {
l = m + 1;
}
}
return cap;
}
// 在 nums 数组上进行偷窃,偷窃的最大能力是 cap,返回最多可以偷窃多少家房屋
private int rob(int[] nums, int cap) {
int res = 0;
for (int i = 0; i < nums.length; i++) {
if (nums[i] <= cap) {
res++;
i++;
}
}
return res;
}
}第 N 个神奇数字
我们不妨考虑第 N 个神奇数字的范围。
首先最小就是 1,因为 n 是从 1 开始的,而最大是 min(a, b) * n,因为对于 a 来说,它的第 n 个神奇数字就是 n * a,更不用说还有 b 的加入会导致第 n 个神奇数字的提前到来。
这里存在的单调性是随着 a ~ b 范围内的数 m 的增大,那么 1 ~ m 范围内的神奇数一定是增加的。
所以我们在 [1, min(a, b) * n] 范围内进行二分,定义函数 f 表示在 1 ~ m 范围内的神奇数的个数,如果个数 ≥ n 那么记录 ans 并且向左二分,否则向右二分。
接下来就是设计函数 f 快速求出 [1...m] 范围内的神奇数的个数。
- [1...m] 范围上能被 a 整数的数字有 m / a 个
- [1...m] 范围上能被 b 整数的数字有 m / b 个
- 当然,这会存在重复的部分(能被 a 和 b 同时整除),所以我们求出 lcm(a, b) 之后将这部分个数减掉
class Solution {
public int nthMagicalNumber(int n, int a, int b) {
long lcm = lcm(a, b);
long l = 1, r = (long) Math.min(a, b) * n, m;
long ans = -1;
while (l <= r) {
m = l + r >> 1;
if (f(m, n, a, b, lcm)) {
ans = m;
r = m - 1;
} else {
l = m + 1;
}
}
return (int) (ans % (1e9 + 7));
}
// [1...m] 能被 a 和 b 整数的数的个数是否 >= n
public boolean f(long m, int n, int a, int b, long lcm) {
return m / a + m / b - m / lcm >= n;
}
public long lcm(int a, int b) {
long gcd = gcd(a, b);
return (a / gcd) * b;
}
public long gcd(int a, int b) {
return b == 0 ? a : gcd(b, a % b);
}
}旋转数组系列题目
轮转数组
这道题目的思路很简单,就是先翻转整个数组,再翻转数组前 k 个元素,最后翻转数组后 n - k 个元素
由于 k 可能会超过 n,所以先对 n 取模,这不会影响结果。
public class RotateArray {
public void rotate(int[] nums, int k) {
int n = nums.length;
k %= n;
reverse(nums, 0, n - 1);
reverse(nums, 0, k - 1);
reverse(nums, k, n - 1);
}
public void reverse(int[] nums, int i, int j) {
while (i < j) {
swap(nums, i++, j--);
}
}
public void swap(int[] nums, int i, int j) {
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
}寻找旋转排序数组中的最小值
首先需要明确的是一个排序数组(无重复),无论旋转多少次,最终的结果一定是一段 or 两段升序序列。
我们使用二分搜索算法,考虑以下情况:
- nums[m] < nums[r]:那么最小值一定在 m 或者 m 左侧,r = m。
- nums[m] > nums[r]:那么最小值一定在 m 右侧,l = m + 1。
- nums[m] = nums[r]:这种情况不可能出现,因为数组没有重复元素。
public int findMin(int[] nums) {
int l = 0, r = nums.length - 1;
int m;
while (l < r) {
m = l + r >> 1;
if (nums[m] < nums[r]) {
// 这里为什么不是 r = m - 1
// 如果 r = m - 1 那么有可能错过最小值(m 就是最小值位置的情况)
r = m;
} else {
l = m + 1;
}
}
return nums[l];
}寻找旋转排序数组中的最小值 II
和上一题的区别在于,该题目的数组不保证去重,也就是可能有重复元素,所以 对 nums[m] = nums[j] 的处理情况有所不同。
我们使用二分搜索算法,考虑以下情况:
- nums[m] < nums[r]:那么最小值一定在 m 或者 m 左侧,r = m。
- nums[m] > nums[r]:那么最小值一定在 m 右侧,l = m + 1。
- nums[m] = nums[r]:这里无法判断 m 在哪个排序数组中,所以让 r 减一,缩小判断范围。
public int findMin(int[] nums) {
int n = nums.length;
int l = 0, r = n - 1;
int m;
while (l < r) {
m = l + r >> 1;
if (nums[m] < nums[r]) {
r = m;
} else if (nums[m] > nums[r]) {
l = m + 1;
} else {
r--;
}
}
return nums[l];
}当 nums[m] = nums[r] 时让 r 减一的正确性推导如下。
当 nums[m] = nums[r] 时,无法判断 m 在左(右)排序数组,自然不能通过二分法安全的缩小区间,比如:
下面两个数组,当 i = 0, j = 4 时,求出的中间位置 m = 2,此时无论选择往左二分还是往右二分都会漏过最优解。
nums1 = 10, 1, 10, 10, 10 // 往右二分会漏过最优解
nums2 = 10, 10, 10, 1, 10 // 往左二分会漏过最优解而要证明 r 减一的正确性,分为两种情况,我们假设旋转点是 x
- 当 x < r 时,即使 r = r - 1,旋转点 x 仍然在区间 [l...r] 内,这是毋庸置疑的,所以可以安全的将 r 减一。
- 当 x = r 是,r = r - 1 会丢失旋转点 x,但是最终返回的 nums[l] 仍然是旋转点值 nums[x],所以也可以安全的将 r 减一。
搜索旋转排序数组
这种方法其实不太好理解,但是这种方式和下面「搜索旋转排序数组 II」是类似的,所以还是需要掌握。
public int search(int[] nums, int target) {
int n = nums.length;
int l = 0, r = n - 1;
int m;
while (l <= r) {
m = l + r >> 1;
// 找到 target 返回
if (nums[m] == target) {
return m;
}
if (nums[l] <= nums[m]) {
// [l, m] 区间是有序的
if (nums[l] <= target && target < nums[m]) {
// target 在 [l, m] 区间内
r = m - 1;
} else {
l = m + 1;
}
} else {
// [m + 1, r] 区间是有序的
if (nums[m] < target && target <= nums[r]) {
// target 在 [m + 1, r] 区间内
l = m + 1;
} else {
r = m - 1;
}
}
}
return -1;
}一个更容易理解的方法:
先通过「寻找旋转数组的最小值」找出旋转点,就可以分离出两段升序区间,在这两段升序区间进行二分即可。
注意,要保证数组元素不能重复。
public int search(int[] nums, int target) {
int n = nums.length;
int l = 0, r = n - 1, m;
while (l < r) {
m = l + r >> 1;
if (nums[m] < nums[r]) {
r = m;
} else {
l = m + 1;
}
}
// l 就是旋转点
// 所以 [0...l - 1] 和 [l...n - 1] 都是升序区间,先找左边,没找到再找右边
int res = binary(nums, l, n - 1, target);
return res != -1 ? res : binary(nums, 0, l - 1, target);
}
public int binary(int[] nums, int i, int j, int target) {
int m;
while (i <= j) {
m = i + j >> 1;
if (nums[m] < target) {
i = m + 1;
} else if (nums[m] > target) {
j = m - 1;
} else {
return m;
}
}
return -1;
}搜索旋转排序数组 II
对于数组中有重复元素的情况,二分查找时可能会有 nums[l] = nums[mid] = nums[r],此时无法判断区间 [l, mid] 和区间 [mid + 1, r] 哪个是有序的。
例如 nums = [3,1,2,3,3,3,3],target = 2,首次二分时无法判断区间 [0, 3] 和区间 [4, 6] 哪个是有序的。
对于这种情况,我们只能将当前二分区间的左边界加一,右边界减一,然后在新区间上继续二分查找。
public boolean search(int[] nums, int target) {
int n = nums.length;
if (n == 0) {
return false;
}
if (n == 1) {
return nums[0] == target;
}
int l = 0, r = n - 1;
int m;
while (l <= r) {
m = l + r >> 1;
if (nums[m] == target) {
return true;
}
// 无法判断区间 [l, mid] 和区间 [mid + 1, r] 哪个是有序的。
// 此时只能将当前二分区间的左边界加一,右边界减一,然后在新区间上继续二分查找。
if (nums[l] == nums[m] && nums[m] == nums[r]) {
++l;
--r;
} else if (nums[l] <= nums[m]) {
// [l, m] 区间是有序的
if (nums[l] <= target && target < nums[m]) {
// target 在 [l, m] 区间内
r = m - 1;
} else {
l = m + 1;
}
} else {
// [m + 1, r] 区间是有序的
if (nums[m] < target && target <= nums[r]) {
// target 在 [m + 1, r] 区间内
l = m + 1;
} else {
r = m - 1;
}
}
}
return false;
}一些总结
可以看到二分还是可以玩出很多花样的,像什么二分答案法,旋转数组这些,最重要的是掌握好最基础的那三种二分方式。
