并查集
2117字约7分钟
2024-10-20
前言
并查集类题目
情侣牵手
针对这道题,有这么几点:
- 首先,对于 rows 数组中的每个人 rows[i],如果对每一对情侣进行编号,那么 rows[i] 就属于第 rows[i] / 2 号情侣。
- 另外,一个显而易见的是,如果 k 对情侣互不相邻,那么将他们交换到相邻的位置至少需要 k - 1 次。
对于第一点,比如第 2 个人和第 3 个人,它们互为情侣,那么他们的情侣编号为 1。
对于第二点,比如目前 rows 数组为 [0, 3, 2, 5, 4, 1],那么这 3 对情侣归位至少需要 2 次,比如 1、3 交换后 5、3 交换。
所以,我们将 rows 数组相邻两个位置的人对应的情侣编号在并查集中进行合并,假设最后并查集有 3 个连通分量,每个连通分量中情侣的对数为 a、b、c,那么将这三个连通分量归为到正确的位置至少的交换次数为 a - 1、b - 1、c - 1,即总的交换次数为 a + b + c - 3。
所以:
- 至少交换的次数 = 情侣的总对数 - 并查集中的连通分量的个数。
class Solution {
public static int MAXN = 31;
public static int[] fa = new int[MAXN];
public static int sets = 0;
public int minSwapsCouples(int[] row) {
int n = row.length;
build(n / 2);
for (int i = 0; i < n; i += 2) {
union(row[i] / 2, row[i + 1] / 2);
}
return n / 2 - sets;
}
public void build(int n) {
for (int i = 0; i < n; i++) {
fa[i] = i;
}
sets = n;
}
public int find(int x) {
return x == fa[x] ? x : (fa[x] = find(fa[x]));
}
public void union(int x, int y) {
int rx = find(x);
int ry = find(y);
if (rx != ry) {
fa[rx] = ry;
sets--;
}
}
public boolean isSameSet(int x, int y) {
return find(x) == find(y);
}
}相似字符串组
其实这道题目的并查集特征很明显,如果两个字符串是相似的,就 union 起来,最后返回并查集中的连通量个数即可。
class Solution {
public static int MAXN = 301;
public static int[] fa = new int[MAXN];
public static int sets = 0;
public int numSimilarGroups(String[] strs) {
int n = strs.length;
int m = strs[0].length();
build(n);
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
if (!isSameSet(i, j)) {
// 如果两个字符串差异字符的个数为 0 or 2 个就视为相似
int diff = 0;
for (int k = 0; k < m && diff < 3; k++) {
if (strs[i].charAt(k) != strs[j].charAt(k)) {
diff++;
}
}
if (diff == 0 || diff == 2) {
union(i, j);
}
}
}
}
return sets;
}
public void build(int n) {
for (int i = 0; i <= n; i++) {
fa[i] = i;
}
sets = n;
}
public int find(int x) {
return x == fa[x] ? x : (fa[x] = find(fa[x]));
}
public void union(int x, int y) {
int rx = find(x);
int ry = find(y);
if (rx != ry) {
fa[rx] = ry;
sets--;
}
}
public boolean isSameSet(int x, int y) {
return find(x) == find(y);
}
}移除最多的同行或同列石头
本题目的一个关键结论:
- 一个二维矩阵,同一行的石头可以算作一个集合,同一列的石头也可以算作一个集合,那么就可以使用并查集做合并。
- 最关键的结论是,在并查集中,每一个连通分量(集合)最后都可以移除到只剩最后一块石头。
- 所以,最终的石头数量就是并查集的连通分量数(集合数),那么可以移除的数量就是总的石头数 - 连通分量数。
import java.util.*;
class Solution {
public static int MAX = 1001;
public static int[] fa = new int[MAX];
public static int sets;
// 第 k 行的第一块石头 v
public static HashMap<Integer, Integer> row = new HashMap<>();
// 第 k 列的第一块石头 v
public static HashMap<Integer, Integer> col = new HashMap<>();
public int removeStones(int[][] stones) {
int n = stones.length;
build(n);
for (int i = 0; i < n; i++) {
int r = stones[i][0];
int c = stones[i][1];
if (!row.containsKey(r)) {
row.put(r, i);
} else {
union(row.get(r), i);
}
if (!col.containsKey(c)) {
col.put(c, i);
} else {
union(i, col.get(c));
}
}
return n - sets;
}
public void build(int n) {
row.clear();
col.clear();
Arrays.fill(fa, 0);
for (int i = 1; i <= n; i++) {
fa[i] = i;
}
sets = n;
}
public void union(int x, int y) {
int rx = find(x);
int ry = find(y);
if (rx != ry) {
fa[rx] = fa[ry];
sets--;
}
}
public int find(int x) {
return x == fa[x] ? x : (fa[x] = find(fa[x]));
}
}打砖块
首先,不会掉落的「砖块」需要满足两个条件:
- 「砖块」位于第 0 行
- 与第 0 行的「砖块」连通
那么我们如何计算每次因击碎砖块而导致其他消失的砖块的数量?
结合下图:
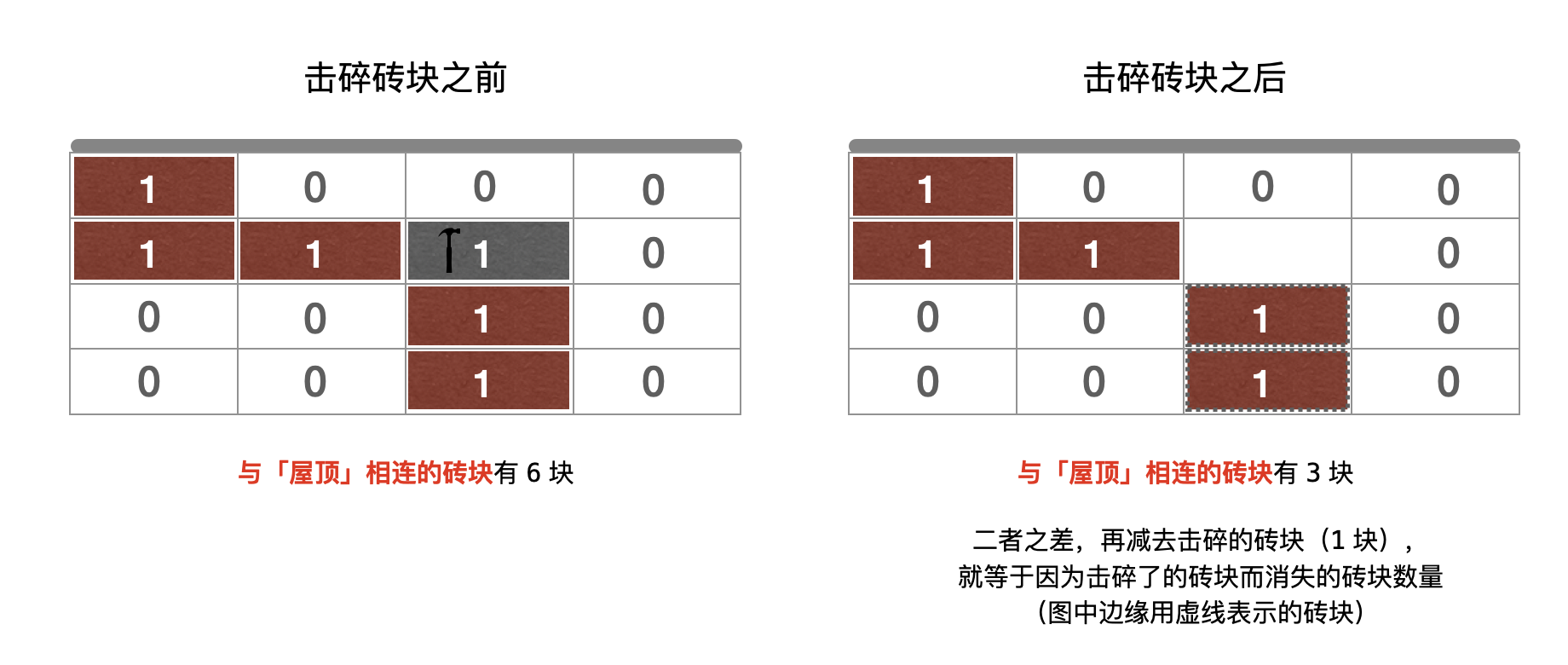
在击碎 (1, 2) 位置的砖块之前,与「屋顶」相连的砖块有 6 块,击碎该砖块之后,(2, 2) 和 (3, 2) 位置的砖块因为没能和「屋顶」连通导致消失,此时与「屋顶」相连的砖块有 3 块。
所以,击碎 (1, 2) 位置的砖块而导致其他砖块消失的数量 = 6 - 3 - 1 = 2。
这其实是一个连通性问题,可以考虑「并查集」。
但是「并查集」主要是将两个连通分量合并为一个连通分量,而击碎一个砖块会导致一个连通分量分为两个连通分量,这提示我们需要反向思考。
即,当逆序补上「被击碎的砖块」之后,有多少个砖块因为这个「被补上的砖块」而重新与「屋顶」相连。
具体步骤,以例子说明。
原始 grid 和 hits 数组如下:

首先,将 hits 数组对应的砖块位置击碎,如下:

接下来,构建并查集,将第 0 行的砖块和「屋顶」合并,将其他行的砖块一一合并。
接下来,逆序补回砖块:
1)此时与「屋顶」相连的砖块有 2 块,补回 [0, 4] 之后

与「屋顶」相连的砖块有 5 块,所以结果是 5 - 2 - 1 = 2
2)此时与「屋顶」相连的砖块有 5 块,补回 [0, 2] 之后

与「屋顶」相连的砖块有 6 块,所以结果是 6 - 5 - 1 = 0
3)此时与「屋顶」相连的砖块有 6 块,补回 [1, 1] 之后

与「屋顶」相连的砖块有 9 块,所以结果是 9 - 6 - 1 = 2
可以看出,当补回完所有砖块,grid 也变为原来的样子。
import java.util.*;
public class Solution {
// 为什么需要 copy 一份原始数组 grid?
// 有可能在逆序补回时,补回的位置原本就是 0,那么就不能再补回一块砖块
int[][] copy;
int row, col;
int[][] dirs = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
public int[] hitBricks(int[][] grid, int[][] hits) {
row = grid.length;
col = grid[0].length;
// 拷贝 copy
copy = new int[row][col];
for (int i = 0; i < grid.length; i++) {
System.arraycopy(grid[i], 0, copy[i], 0, col);
}
// 根据 hits 数组将 copy 数组中的砖块置为 0,后续补回
for (int[] hit : hits) {
copy[hit[0]][hit[1]] = 0;
}
// 创建并查集
int top = row * col; // 天花板
UnionFind uf = new UnionFind(top + 1);
// 将第 0 行的砖块与天花板合并
for (int j = 0; j < col; j++) {
if (copy[0][j] == 1) {
uf.union(j, top);
}
}
// 将后续的砖块一一合并
for (int i = 1; i < row; i++) {
for (int j = 0; j < col; j++) {
if (copy[i][j] == 1) {
// 上
if (copy[i - 1][j] == 1) {
uf.union(i * col + j, (i - 1) * col + j);
}
// 左
if (j > 0 && copy[i][j - 1] == 1) {
uf.union(i * col + j, i * col + (j - 1));
}
}
}
}
// 根据 hits 数组逆序补回
int[] res = new int[hits.length];
for (int i = hits.length - 1; i >= 0; i--) {
int x = hits[i][0];
int y = hits[i][1];
// 如果在补回的位置原来就是 0,那么就不能再补回
if (grid[x][y] == 0) {
continue;
}
// 计算补回之前与天花板相连的个数
int before = uf.getSize(top);
// 如果补回位置是在第 0 层,则与天花板合并
if (x == 0) {
uf.union(y, top);
}
// 四个方向依次看是否可以进行合并
for (int[] dir : dirs) {
int nx = x + dir[0];
int ny = y + dir[1];
if (nx >= 0 && nx < row && ny >= 0 && ny < col && copy[nx][ny] == 1) {
uf.union(x * col + y, nx * col + ny);
}
}
// 真正补回
copy[x][y] = 1;
// 计算补回之后与天花板相连的个数
int curr = uf.getSize(top);
// 补回的位置没有和天花板合并,也就是 curr = before,那么 res[i] = 0
res[i] = Math.min(curr - before - 1, 0);
}
return res;
}
public static class UnionFind {
int[] fath;
int[] size;
public UnionFind(int x) {
fath = new int[x];
size = new int[x];
for (int i = 0; i < x; i++) {
fath[i] = i;
size[i] = 1;
}
}
public void union(int x, int y) {
int rx = find(x);
int ry = find(y);
if (rx == ry) {
return;
}
fath[rx] = ry;
size[ry] += size[rx];
}
public int find(int x) {
if (x == fath[x]) {
return x;
}
return fath[x] = find(fath[x]);
}
public int getSize(int x) {
return size[find(x)];
}
}
}